Spherical coordinates¶

Orientation-related commands (e.g. cylinderorientation) use spherical coordinates defined in the figure below. Namely, \(\phi\) refers to the azimuthal angle and \(\theta\) to the polar angle. The azimuthal angle is measured in \(xy\)-plane from the positive \(x\)-axis towards the positive \(y\)-axis, and its values are always in the range \([-\pi, \pi]\). The polar angle is measured from the positive \(z\)-axis towards the \(xy\)-plane, and its values are always in the range \([0, \pi]\).

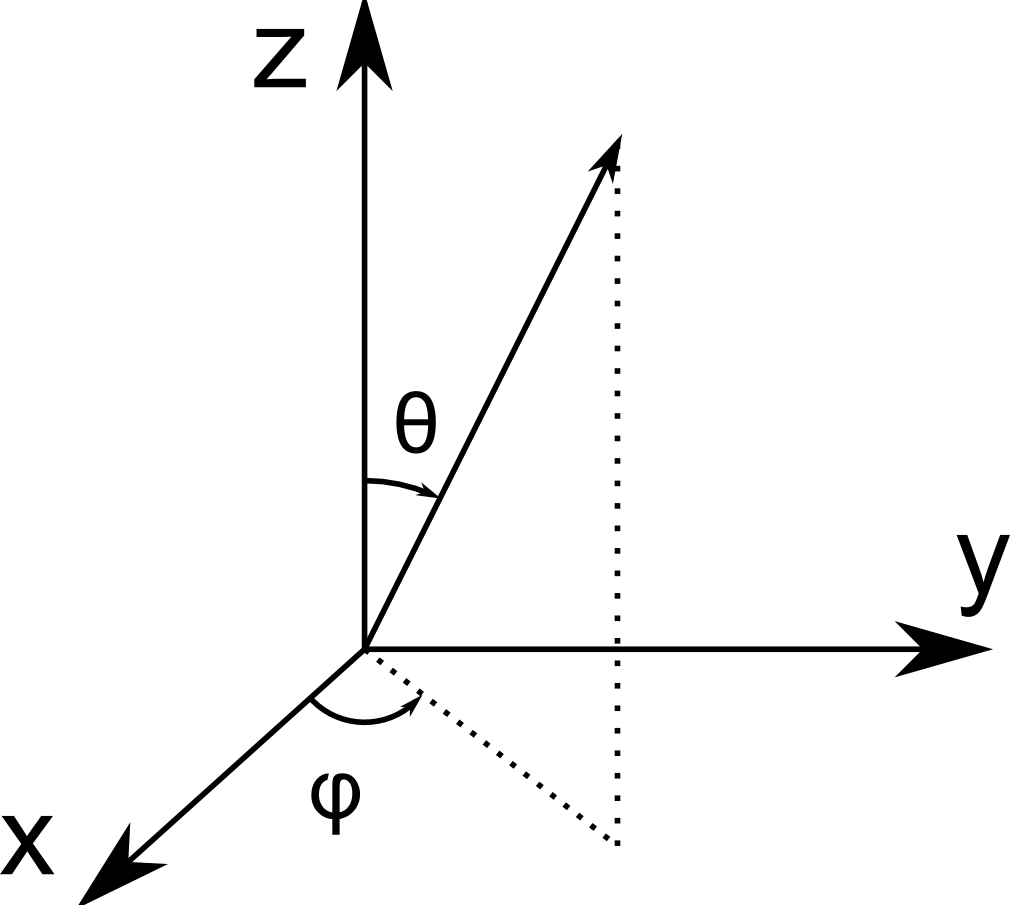
Spherical coordinate system used in pi2. Here, \(\phi\) is the azimuthal angle and \(\theta\) is the polar angle.

Conversion from the cartesian coordinates to the polar coordinates is done with

\[\begin{split}r &= \sqrt{x^2 + y^2 + z^2} \\ \phi &= \operatorname{arctan2}(y, x) \\ \theta &= \arccos(z / r)\end{split}\]

Conversion from the polar coordinates to the cartesian coordinates is done with

\[\begin{split}x &= r \cos(\phi) sin(\theta) \\ y &= r \sin(\phi) sin(\theta) \\ z &= r \cos(\theta)\end{split}\]

Most orientation-related commands return only angles for which the cartesian \(x\)-component is positive. This is because the orientations are symmetrical, i.e. directions \(-\vec{r}\) and \(\vec{r}\) describe the same orientation, and therefore half of the possible directions are redundant. Additionally, in orientation-related commands \(r=1\) most of the time.